• Concepts relationnels
• Opérations usuelles
  • détails des opérations
  • application sur un exemple simple

Qu’est-ce qu’une base de données ?

Ensemble de données simples (dites atomiques) réparties dans des tables et reliées entre elles, permettant le fonctionnement d’une organisation, d’une entreprise via une ou plusieurs applications informatiques.

• Ensemble de données non indépendantes,
• Interrogeable par le contenu (selon des critères),
• Structure retrouvable.

SGBD : Système de Gestion de Bases de Données

Ensemble des logiciels permettant aux utilisateurs d’insérer, de modifier et de rechercher efficacement des données spécifiques dans une grande masse d’informations partagée par de multiples utilisateurs.

Objectifs du modèle

• Indépendance des programmes avec la représentation interne des données,
• Traitement des problèmes de cohérence et de redondance des données,
• Utilisation de langages de manipulation de données non procéduraux,
• Extensibilité du modèle pour des données complexes,
• Standardisation pour la description et la manipulation des bases de données.

Domaine : Ensemble de valeurs caractérisées par un nom

Cardinal : Nombre d’éléments d’un domaine

Quelques exemples de domaines usuels :

Entier : 0, 1, 5, -4, 1324587, ...
Réel : 1.5, 3.14, -5.09, 10654.241687, 0.00000001, ...
Chaîne de caractères : "abcdef", "bonjour vous", "1", ...
Sexe : "H", "F" (ici, cardinal = 2)
Date : nombre de jours depuis une date de référence 

Produit cartésien : Ensemble des n-uplets (\(d_1, d_2, \ldots, d_n\)) où chaque \(d_i\) est un élément du domaine \(\mathbf{D}_i\)

Si on a un premier attribut Code dont le domaine est {1, 2, 3, 4} (cardinal = 4) et un autre TVA de domaine {0, 5, 10} (cardinal = 3), le produit cartésien des deux domaines Codes X TVA aura un cardinal de 12 (4 * 3) et prendra les valeurs suivantes :

{
    (1, 0), (2, 0), (3, 0), (4, 0), 
    (1, 5), (2, 5), (3, 5), (4, 5), 
    (1,10), (2,10), (3,10), (4,10)
}

• Relation (ou table) : Sous-ensemble du produit cartésien d’une liste de domaines
• Attribut : Colonne d’une relation
• Tuple : Ligne d’une relation correspondant à un enregistrement
• Schéma : Nom suivi de la liste des attributs et de la définition de leurs domaines.

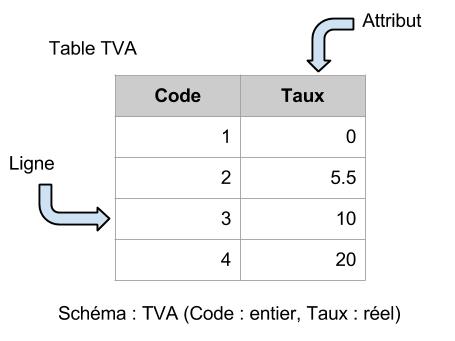
Description d’une table

Contrainte de domaine

• Permet de définir l’ensemble de valeurs possibles pour chaque attribut
• Important pour limiter les erreurs (mettre un caractère dans un entier par exemple)
• Attention à ne pas trop restreindre (choisir un entier alors qu’il est possible qu’à l’avenir il y ait des réels par exemple)

Unicité de la clé

• Attribut (ou groupe d’attributs) permettant d’identifier chaque ligne de la table de manière unique
• Soit naturel (par exemple numéro de sécurité sociale), soit automatique
• Cela permettra de faire des liens entre lignes de plusieurs tables sans ambiguïté
• On parle aussi de clé primaire

Contrainte d’entité

• Une clé primaire ne peut pas avoir de valeur NULL (non-présence de l’information)
• Il doit absolument y avoir une valeur pour l’attribut, ou pour chaque attribut dans le cas d’une clé multiple

Contrainte de référence

• Attribut(s) d’une relation devant apparaître comme clé dans une autre relation
• On doit bien évidemment indiquer la table, et le nom de l’attribut (si celui-ci n’a pas le même nom)
• On parle aussi de clé externe

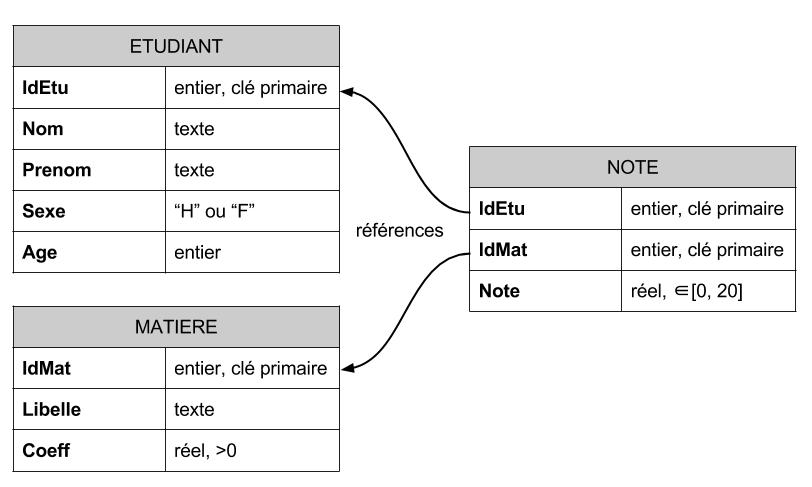
Schéma de la base de données Exemple

Table : Etudiant 

  IdEtu      Nom    Prenom Sexe Age
1     1    Remin   Norbert    H  19
2     3 Constant Raphaelle    F  20
3     4  Fleurot  Isabelle    F  19
4     5   Yannic  Sandrine    F  18
5     6    Josse   Francis    H  20

Table : Matiere 

  IdMat Libelle Coeff
1     1   Maths   1.0
2     2   Stats   3.0
3     3     Com   1.0
4     5     SQL   2.5

Table : Note 

  IdEtu IdMat Note
1     3     1   12
2     3     5   15
3     4     5    2
4     4     2    9
5     4     1    7
6     1     1   18
7     1     2   11
8     1     5    5
9     6     1    9

• Sur une table :
  • Restriction
  • Projection
  • Calcul ou fonction
  • Agrégat
• Sur deux tables ayant le même schéma (i.e. les mêmes colonnes) :
  • Union, Intersection, Différence
• Sur deux tables quelconques :
  • Jointure

Sélection de lignes d’une table, sur la base d’une condition à respecter (cette condition peut être une combinaison de comparaison à l’aide de AND et de OR - attention aux parenthèses dans ce cas)

• Restriction sur Age >= 19, sur la table Etudiant

 IdEtu      Nom    Prenom Sexe Age
     1    Remin   Norbert    H  19
     3 Constant Raphaelle    F  20
     4  Fleurot  Isabelle    F  19
     6    Josse   Francis    H  20

Sélection de colonnes d’une table, sur la base d’une liste d’attributs

• Projection sur Prenom et Sexe, sur la table Etudiant

    Prenom Sexe
   Norbert    H
 Raphaelle    F
  Isabelle    F
  Sandrine    F
   Francis    H

Opération artihmétique, fonction mathématique, fonction sur chaîne de caractères, …

• Calcul de l’année de naissance (2015 - Age), dans la table Etudiant

 IdEtu      Nom    Prenom Sexe Age 2015 - Age
     1    Remin   Norbert    H  19       1996
     3 Constant Raphaelle    F  20       1995
     4  Fleurot  Isabelle    F  19       1996
     5   Yannic  Sandrine    F  18       1997
     6    Josse   Francis    H  20       1995

Calcul statistique (somme, moyenne, nombre de valeurs, …) sur un attribut, éventuellement en fonction des valeurs d’un autre attribut

• Calcul de la moyenne d’âge globalement, puis par sexe

 AVG(Age)
     19.2

 Sexe AVG(Age)
    F     19.0
    H     19.5

Création de deux tables pour opérations ensemblistes :

• A : Etudiants masculins (restriction à Sexe = "H")

 IdEtu   Nom  Prenom Sexe Age
     1 Remin Norbert    H  19
     6 Josse Francis    H  20

• B : Etudiants de 20 ans (restriction à Age = 20)

 IdEtu      Nom    Prenom Sexe Age
     3 Constant Raphaelle    F  20
     6    Josse   Francis    H  20

Ensemble des lignes présentes dans l’un et/ou l’autre des deux tables, celles devant avoir les mêmes colonnes

• \(A \cup B\) : étudiants masculins ou ayant 20 ans (ou les deux)

 IdEtu      Nom    Prenom Sexe Age
     1    Remin   Norbert    H  19
     6    Josse   Francis    H  20
     3 Constant Raphaelle    F  20
     6    Josse   Francis    H  20

une même ligne peut être présente dans les deux tables : à gérer si on veut ne l’avoir qu’une seule fois

Ensemble des lignes présentes dans les deux tables simultanément, celles devant avoir les mêmes colonnes

• \(A \cap B\) : étudiants masculins et ayant 20 ans

 IdEtu   Nom  Prenom Sexe Age
     6 Josse Francis    H  20

L’union et l’intersection sont commutatives au contraire de la différence (cf ci-après)

Ensemble des lignes présentes dans la première table et absentes dans la deuxième table, les deux devant avoir les mêmes colonnes

• \(A \setminus B\) : étudiants masculins n’ayant pas 20 ans

 IdEtu   Nom  Prenom Sexe Age
     1 Remin Norbert    H  19

• \(B \setminus A\) : étudiants de 20 ans n’étant pas masculin

 IdEtu      Nom    Prenom Sexe Age
     3 Constant Raphaelle    F  20

Association de chaque ligne de la première table avec chaque ligne de la deuxième table

• Produit cartésien entre IdMat et IdEtu

 IdMat IdEtu
     1     1
     1     3
     1     4
     1     5
     1     6
     2     1
     2     3
     2     4
     2     5
     2     6
     3     1
     3     3
     3     4
     3     5
     3     6
     5     1
     5     3
     5     4
     5     5
     5     6

Restriction d’un produit cartésien aux lignes respectant une condition (le plus souvent égalité de deux attributs ayant le même nom)

• Jointure naturelle entre Note et Matiere

 IdEtu IdMat Note Libelle Coeff
     3     1   12   Maths   1.0
     3     5   15     SQL   2.5
     4     5    2     SQL   2.5
     4     2    9   Stats   3.0
     4     1    7   Maths   1.0
     1     1   18   Maths   1.0
     1     2   11   Stats   3.0
     1     5    5     SQL   2.5
     6     1    9   Maths   1.0

• Organisées dans des tables différentes,

• Absolument nécessité des jointures.

• Jointure naturelle : la restriction est sur l’égalité des attributs ayant le même nom entre les deux tables ;

• Jointure interne : on ne garde que les lignes ayant des informations dans les deux tables ;

• Jointure externe gauche (et respectivement droite) : on garde aussi les lignes de la table de gauche (resp. de droite) qui n’ont pas de connexion avec une ligne de l’autre table ;

• Jointure externe complète : toutes les lignes des deux tables sont conservées.

• Jointure externe gauche entre Etudiant et Note

 IdEtu      Nom    Prenom Sexe Age IdEtu IdMat Note
     1    Remin   Norbert    H  19     1     1   18
     1    Remin   Norbert    H  19     1     2   11
     1    Remin   Norbert    H  19     1     5    5
     3 Constant Raphaelle    F  20     3     1   12
     3 Constant Raphaelle    F  20     3     5   15
     4  Fleurot  Isabelle    F  19     4     1    7
     4  Fleurot  Isabelle    F  19     4     2    9
     4  Fleurot  Isabelle    F  19     4     5    2
     5   Yannic  Sandrine    F  18    NA    NA   NA
     6    Josse   Francis    H  20     6     1    9

L’étudiante n’ayant pas de note est conservée mais des valeurs NULL (indiquées par des NA ici)

• Prénom, libellé de la matière et note obtenue, trié par matière
  • 2 jointures
  • Projection

    Prenom Libelle Note
 Raphaelle   Maths   12
  Isabelle   Maths    7
   Norbert   Maths   18
   Francis   Maths    9
 Raphaelle     SQL   15
  Isabelle     SQL    2
   Norbert     SQL    5
  Isabelle   Stats    9
   Norbert   Stats   11

• Matière et moyenne, par ordre décroissant de moyenne
  • 2 jointures
  • Calcul d’agrégat
    • Tri

 Libelle Moyenne
   Maths    11.5
   Stats    10.0
     SQL     7.3

Possibilité (quasi-infinie) de combiner toutes les opérations

SELECT { attribut | expression | fonction } [, ... ]
    FROM table [, ...]
    WHERE condition(s)
    GROUP BY attribut(s)
    HAVING condition(s) 
    ORDER BY attribut(s)/nombre(s);

• Les jointures se font dans le FROM ;
• La clause WHERE permet de faire les restrictions ;
• Les projections se font dans le SELECT ;
• Les calculs et agrégats sont à faire dans le SELECT, avec les attributs de regroupement d’agrégat dans le GROUP BY ;
• Il est possible de faire des conditions spécifiques sur ces agrégats dans le HAVING ;
• On peut effectuer un tri du résultat dans la partie ORDER BY.

subset(table, subset = condition(s), select = attribut(s))
transform(table, attribut = expression(s))
aggregate(attribut ~ attribut(s), table, fonction)
merge(table, table, ...)

• Les projections et restrictions peuvent se faire avec la fonction subset ;
• Les calculs se font dans la fonction transform ;
• Tout ce qui est calcul d’agrégat est à faire avec la fonction aggregate ;
• Les jointures se font dans la fonction merge.

Il est souvent possible de réaliser des opérations selon la logique relationnelle et d’autres selon une logique plus spécifique au langage R. Il est présenté ici les fonctions orientées relationnel.

data table;
    merge table table;
    attribut = expression;
    where condition(s);
    keep | drop attribut(s);
run;
proc means | freq;
run;

• La clause merge permet de déterminer les tables pour les jointures ;
• Les projections se font dans le keep ou le drop ;
• Les restrictions sont détaillées dans le where ;
• Les calculs classiques se font dans l’étape data et les agrégats dans une procédure summary, means ou freq.

Idem que pour R, différentes voies sont parfois possibles.

Interrogation de données avec :

• SQL
• R
• SAS
• MongoDB